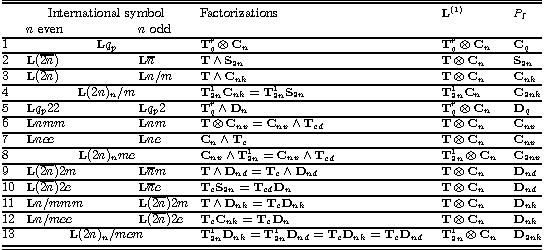
| For each of 13 family of the line groups different factorizations in
the form L=ZP are given (Z is
infinite cyclic group of generalized translations - pure translations
T,
screw axis Trq or glide plane Tc,
and P is axial point group). The maximal first family subgroup
and isogonal point group PI, are presented (n
is the order of the principle rotational axis of
P, andq
of
PI). Here, Tcd denotes
the glide plain bisecting the angle between vertical mirror planes in P.
For the groups of the families 1 and 5, q is multiple of n
(p from the international symbol is function of n, q
and r) |
| Za svaku od 13 familija linijskih grupa date su razlicite faktorizacije
u formi L=ZP (Z je beskonacna
ciklicna grupa generalisanih translacija - ciste translacije T,
zavojna osa Trq ili klizna ravan
Tc,
a P je asijalna tackasta grupa). Slede, maksimalna podgrupa
iz prve familije i izogonalna tackasta grupa
PI
(n je red glavne ose u P,
a q u PI).
Tcd je klizna ravan na simetrali ugla koji cine
vertikalne ravni refleksije u P. Za groupe familija 1 i 5,
q
je umnozak n (p iz internacionalnog simbola je funkcija n,
q
i r) |